Penrose Tiling

Semi- Regular Tessellations: Shape 1

Multiple Tessellations

Tessellation: Polygon

Enlarged Quadrilateral

The enlargement factor was 1/2. When you divide the area of the image by the area of the original quadrilateral the answer is 0.25, this means that the image is one quarter of the original's size.

Unchanged (Invariant): Angles, Shape.
Changed: Side lengths, Area, Sense/Orientation.

Enlargement 2

When you divide the area of the image by the area of the original shape the outcome is the enlargement factor multiplied by itself. This is proven the when the enlargement factor was 3, the answer was 9. With this information we can then predict that if the enlargement factor was 4 the area of the image divided by the area of the original shape would be 16, and if the enlargement factor was 5, the outcome would be 25.

Enlargement

I have found that although the lengths of the sides of the enlarged triangle had increased, the angles had remained invariant.

Properties of Translation

Angles are invariant under a translation.

The lengths of the sides of an object are invariant under a translation.

There are 6 invariant points.

Tesellation

Transformations

The co-ordinates of each vertex of the translated triangle are; (6,1) (6,-1) (1,-3)

The vector required to finish the simple red design was -2-2.

Olympic Rings

Triangle and Rotation Answers

From the triangle beside, we can see that both the original triangle and the rotated share that point which it was rotated on.

The actual shape remains the same (invariant) which means that the shape has been unaltered, merely rotated.

All the angles in comparison between the original triangle and rotated triangle were the same, there was no change in the angles post rotation. This can be proven by moving around the points of the original triangle and it's image will follow.

The lengths, like the angles, did not change upon rotation, they were also the same in comparison between the original and rotated triangles.

Angles are invariant under a rotation.
The lengths of the sides of an object are invariant under a rotation.
The centre of rotation is the only invariant point.

Mitsubishi Logo

Rotation: L & H

Rotation: Quadrilateral

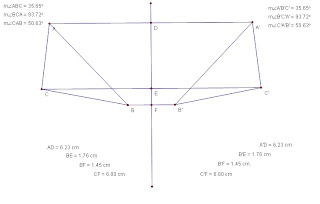
The distances of the reflected shape and the original shape remain the same from point to point.

No matter where are vertex is, the angles of both shapes are still equal.

When animated, the distances between AD and A'D remain the same.

All the distances in pairs (eg AD and A'D) are all the same.

Angles are invariant under a reflection.
The lengths of the sides of an object are invariant under a reflection.
Points on the mirror line are invariant under a reflection.


I have found that all angles and all distances and measurements were invariant between original shapes and reflected shapes everything was the same except that the shape was reversed.

Reflection: F, Tree, and Shape.

Reflection: Triangle

The labeling system shows that when you mirror the object the labeled points are reversed.

When the mirror line passes through the base of the original triangle, the mirrored triangle is partially inside the original one

When a point of the original object is on the mirror line, it is called an invariant point.

Line Functions: Task 4

x-6
-x-2
-4x-11

Line Functions: Task 3

2x-3

Line Functions: Task 2

Line Functions: Task 1

Opposite Angles in Cyclic Quadrilaterals

The opposite angles of a cyclic quadrilateral sum to 180°.

Tangent Perpendicular to the Radius

A tangent to a circle meets the radius at 90° at the point of contact.

Angles on the Same Arc

Angles at the circumference standing on the same arc are equal.

The Angle in a Semi-circle

The angle in a semi-circle is a right angle.

Angles at the center of a circle

The angle at the centre of a circle is twice the angle at the circumference standing on the same arc.

• The sum of the exterior angles of a hexagon is 360°.
• The sum of the interior angles of a hexagon is 720°.
• The angles at a point sum to 360°.

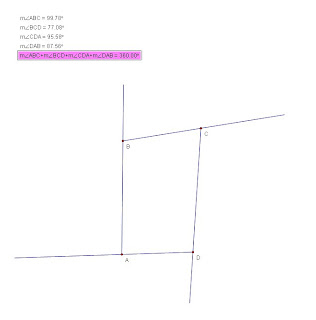
Interior/Exterior angle of a Quadrilateral

• The interior angle sum of a quadrilateral is 360°.
• The exterior angle sum of a quadrilateral is 360°.

Angles and parallel angles.

• When a pair of parallel lines are cut by a transversal:

1) the corresponding angles are equal,

2) the alternate angles are equal,

3) the co-interior angles are supplementary.

• Supplementary angles are angles which sum to 180°.

Exterior angles of a triangle

The exterior angle of a triangle the sum of its interior opposite angles.

Angle sum of a triangle.

• The angle sum of a triangle is 180°.

Angles in a line.

• If two angles sum to 180 º they are called supplementary angles.
• When two lines intersect, the vertically opposite angles are equal.
• The angle sum of a straight line is 180º.